Whether it’s finding the nearest pick-up point, planning your commute, or choosing a location for your future office or store, navigation is essential for numerous everyday and business tasks. And this is where map services come in. They visualize the terrain, showing the location of various places and interconnections between them.
This isn’t an easy task. After all, the screens of smartphones, tablets, and PCs used to access these services are flat. The Earth’s surface, on the other hand, is not. To visualize it, you need to project the complex geoid shape of the planet onto a plane.
Let’s find out how this is done and explore the differences between the resulting projections. We’ll also learn what types of projections are used in popular online map services.
Types of projections
Imagine a room with a globe in its center. A light bulb shines out from within the globe. The shadows cast onto the walls would be the Earth’s projection, with every point on the globe having a corresponding point on the surface.
Depending on the type of projection, the shape of its center (the light bulb) and projection surface (the room) can vary. This influences the accuracy of the resulting representation.
However, no single projection can simultaneously preserve the correct angles, distances, and areas of geographical objects. For this reason, your choice of projection should always depend on the task at hand.
Azimuthal projections
Azimuthal projections preserve the angles between directions on a map but distort distances and areas.
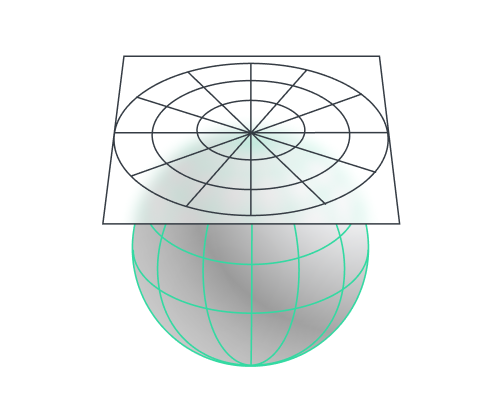
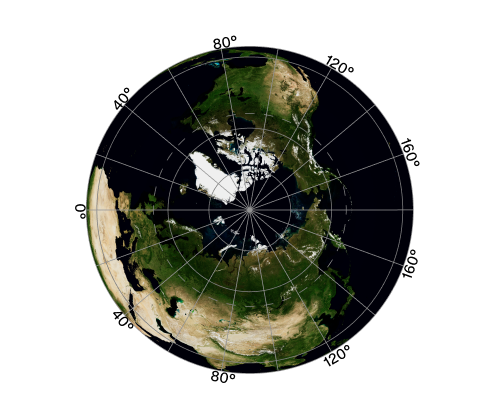
This type of projection involves mapping points on the Earth’s surface onto a tangent plane. Though the representation doesn’t have any distortion at the tangent point, it gets progressively more distorted as you move away.
The ray can originate either from the surface itself or from the planet’s center, in which case only one hemisphere can be mapped onto the plane.
In practice, azimuthal projections are used to show the direction of winds and currents, and for working with satellite ground stations with directional antennas (see azimuthal equidistant projection).
Conic projections
Conic projections preserve shapes and distances within a small area.
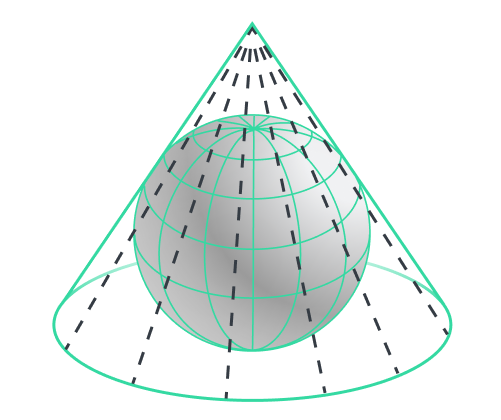
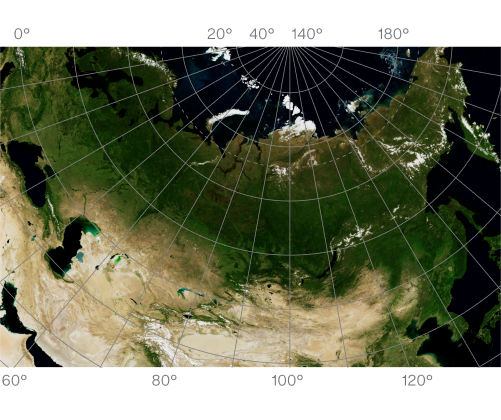
In projections of this type, points on the Earth’s surface are mapped onto the surface of a cone. There’s no distortion in the vicinity of the tangent line, but it starts to appear and significantly intensifies as you approach the cone’s base or apex. This type of projection is widely used in aviation for planning flights in certain parts of the world. The reason is that conic projections can show great-circle distances as straight lines (see Lambert projection). These straight lines represent the shortest distance between the points they connect on the globe.
Cylindrical projections
Cylindrical projections can preserve both the shape of objects and the distances between them.
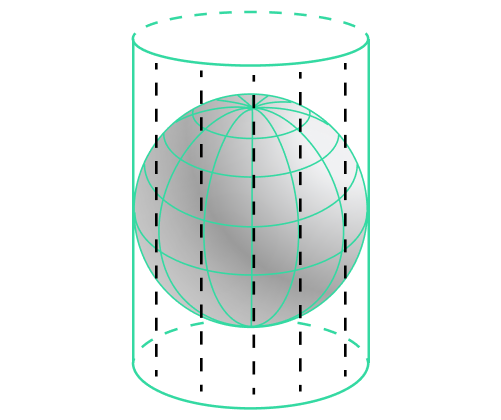
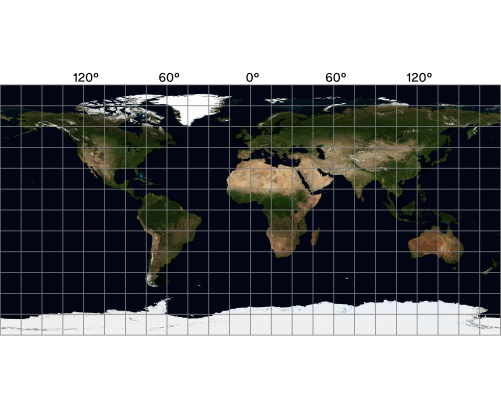
In projections of this type, points on the Earth’s surface are mapped onto the surface of a cylinder. There is no distortion in the vicinity of the tangent line, but it starts to appear and significantly intensifies as you approach the cylinder’s bases. Cylindrical projections, such as the Mercator projection, are used in navigation because of their ability to represent rhumb lines as straight lines. This means that if you choose an azimuth from a point on the map and start moving along it, all points will lie on the same straight line. The drawback of this type of projection is that the areas of map objects become greatly distorted as you approach the poles. For example, this makes Greenland appear larger than Africa. Due to extreme distortion, the poles themselves can’t always be mapped.
Polyhedral projections
Polyhedral projections break the Earth into flat faces, preserving the shapes within each face.
The projections from these examples map the globe onto a truncated octahedron with symmetrical faces, which can be displayed in a variety of configurations.
Projections of this type are very difficult to create, display, and position.
Popular projections
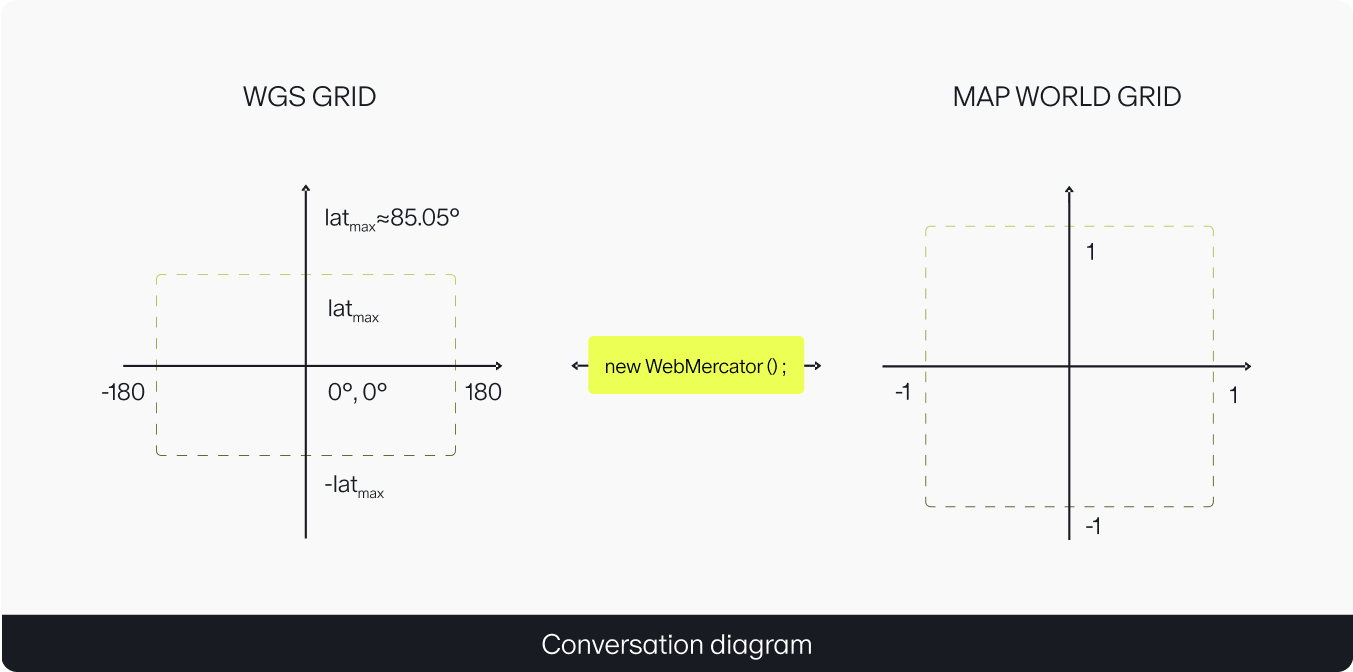
For world maps, the majority of services use cylindrical projections. Most often, it’s the WGS 84 Web Mercator EPSG:3857. In these projections, the Earth is assumed to be a sphere, and the poles are truncated beyond the latitude of ±85.05113°.
The Web Mercator is used by several online map services, including Google Maps, Mapbox, Leaflet, ArcGIS, and Waze.
For convenience, we also use it for JavaScript API maps.
World Geodetic System (WGS)
The location of objects on the Earth’s surface can be described using the World Geodetic System, a universally adopted geographic coordinate system.
The WGS uses horizontal rings (parallels) and vertical semicircles (meridians) to divide the globe into sectors. In this system, the reference axes are the zero meridian and the zero parallel (the equator).
Latitude and longitude, both of which are angular measurements, originate from these axes.
- Latitude represents the position of an object relative to the equator. It’s measured in degrees from 0° to 90°, which can be north (N) or south (S).
- Longitude defines the position of an object relative to the prime meridian. It’s measured in degrees from 0° to 180°, which can be east (E) or west (W).

The latest standard of this coordinate system, WGS 84, defines the points of reference and parameters for mapping the physical world:
- The center of the Earth is located at the globe’s center of mass.
- The polar radius is roughly 6356.75 km, and the equatorial radius about 6378.14 km.
- The zero parallel is located on the plane that passes through the Earth’s center of mass.
- The prime meridian is approximately 102 meters to the right of the Royal Observatory in Greenwich, allowing for the smallest vertical deflection from the Earth’s center of mass.
The WGS allows for fairly precise positioning of any object on the Earth’s surface. And this is where we circle back to projections. It’s projections that help us convert WGS coordinates to meters on the Earth’s surface and vice versa. However, this alone isn’t enough to display objects on the user’s device. You also need a way to convert these WGS coordinates into screen pixels. Furthermore, the number of pixels can vary significantly between different screens. This is why we introduced the World Coordinates System for the JavaScript API, which offers an additional level of abstraction.
World Coordinates System for the JavaScript API
The JS API World Coordinates System is a normalized coordinate grid with values ranging from –1 to 1 on both axes.
This time, the task of the projection is to reconcile the WGS with the JS API World Coordinates System system. Then, based on the user’s device and its display size, the map translates the JS API World Coordinates System into screen pixels.
This way, you can render maps in any coordinate system and on any screen, regardless of their parameters.
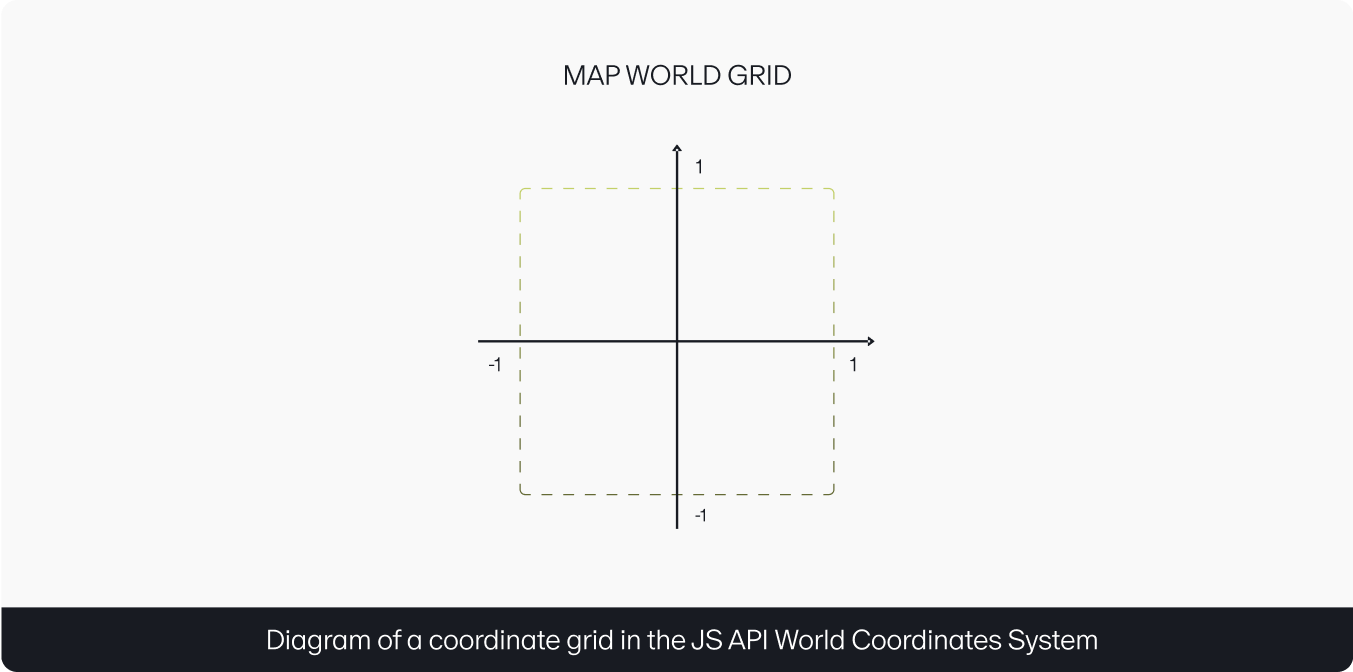
The API user only needs to specify a projection once. After this, they can work using the coordinate system of their choice. The API adjusts all map components to the selected system automatically.
Web Mercator module
As mentioned before, the JavaScript API uses the Web Mercator by default. This projection is also available as the mappable-web-mercator-projection package. Let’s take a look at its logic.

With this projection, you can display data on maps from a variety of open sources, like OSM and OpenRailwayMap. This package can be useful on the server side — to load data for specific tiles, for example. To learn more, see our “Displaying a large number of objects on a map” post.
Now you know the main differences between the various types of projections and are ready for a deeper dive into their specifics. By the way, you can use projections both to represent the surface of the Earth, and for office layouts and construction blueprints. More about this in our future posts.
*The satellite maps in this article are provided by the NASA Earth Observatory and are intended for informational and educational purposes only.
MAX PIN, JS API developer


